ING. LUIS MANFREDO REYES
1. INTRODUCCION: Los valores y vectores propios, son propiedades importantes de las matrices cuadradas de tamaño nxn y tienen aplicaciones en el cálculo y la estadística. En éste documento se estudiará el uso de GEOGEBRA para el cálculo de valores y vectores propios,
Para detalles sobre el calculo manual de valores y vectores propios, y sus aplicaciones se puede consultar:
http://reyesestadistica.blogspot.com/2013/04/calculo-de-valores-y-vectores-propios-y.html
http://reyesestadistica.blogspot.com/2013/04/calculo-de-valores-y-vectores-propios-y.html
GeoGebra es un software matemático. Fue creado con la idea de ser usado para la educación en colegios y universidades. Fue creado por Markus Hohenwarter, en el año 2001 en la Universidad de Salzburgo, luego en la Universidad de Atlantic, Florida, luego en la Universidad Estatal de Florida y actualmente , en la Universidad de Linz, Austria.
El software tiene dos partes importantes: un procesador geométrico y un procesador algebraico.
GeoGebra permite el trazado de construcciones geométricas de todo tipo así como la representación gráfica, el tratamiento algebraico y el cálculo de funciones reales de variable real, sus derivadas, integrales, etc.
DISPONIBILIDAD:
Existen versiones para: Windows, Linux, MacIntosh, Android e Ios.
Existen algunas diferencias entre las versiones, pero la mayoría de aspectos son iguales.
La última versión disponible es la 5.
Geogebra no posee comandos directos para calcular valores propios (eigenvalues) o vectores propios (eigenvectors), pero el procedimiento se puede realizar utilizando las hojas de trabajo desarrolladas por los usuarios
PARA MATRICES 2X2: https://www.geogebra.org/m/N78q77VK
PARA MATRICES 3X3: https://www.geogebra.org/m/ZJtywDTd
Autor Lee Robinson
PARA MATRICES 2X2: https://www.geogebra.org/m/N78q77VK
PARA MATRICES 3X3: https://www.geogebra.org/m/ZJtywDTd
Autor Lee Robinson
Ejemplo
Calcular los valores y vectores propios de la matriz:
Cargar la hoja de tabajo: https://www.geogebra.org/m/rMXd7p3V
Ingresar los valores en la parte inferior, al lado del boton RESET y luego dar click en este boton:
El deslizador del lado derecho debe moverse hacia abajo para mostrar las operaciones realizadas:
Los valores propios son -1 y 2
Los vectores propios son S1 y S2 y sus multiplos
En la parte grafica se pueden ver los vectores proyectados en el plano.
ejemplo con una matriz 3x3
Cargar la hoja de trabajo: https://www.geogebra.org/m/ZJtywDTd
En la parte inferior ingresar la matriz y oprimir el boton RESET
El deslizador de la izquierda moverlo al fondo para mostrar las operaciones realizadas:
los valores propios son -1, 3, 4
y los vectores propios son s1,s2,s3 y sus multiplos
PROCEDIMIENTO MANUAL:
Cargar la hoja de tabajo: https://www.geogebra.org/m/rMXd7p3V
Ingresar los valores en la parte inferior, al lado del boton RESET y luego dar click en este boton:
El deslizador del lado derecho debe moverse hacia abajo para mostrar las operaciones realizadas:
Los valores propios son -1 y 2
Los vectores propios son S1 y S2 y sus multiplos
En la parte grafica se pueden ver los vectores proyectados en el plano.
ejemplo con una matriz 3x3
Cargar la hoja de trabajo: https://www.geogebra.org/m/ZJtywDTd
En la parte inferior ingresar la matriz y oprimir el boton RESET
El deslizador de la izquierda moverlo al fondo para mostrar las operaciones realizadas:
los valores propios son -1, 3, 4
y los vectores propios son s1,s2,s3 y sus multiplos
PROCEDIMIENTO MANUAL:
Se puede realizar el calculo en forma manual, aplicando una serie de operaciones matriciales y algebraicas. EL PROCEDIMIENTO SE REALIZA EN LA VISTA CAS, la cual no esta disponible en tablets ni telefonos.
Ejemplo: (obtenido en Geogebra Tube)
2. Ingresar la matriz identidad 2x2: p={{1,0},{0,1}}
3. Realizar la operacion: q-t*p
4. Calcular la determinante del resultado: Determinante[$1}
5. Igualar a cero y resolver: Soluciones[$2=0,t]
6. Seleccionar el primer elemento de la respuesta: Elemento[$3,1]
7. Formar el vector x,y que contendra los valores propios: Vector[x,y]
8. Operar q*el vector x,y: q*$5
9. Operar $4*$5 y resolver el sistema
Los valores propios son: 1.27 y 4.73
Vectores propios (3,1.73) y (3,1.73)











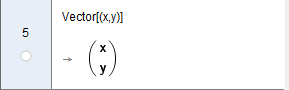



No hay comentarios:
Publicar un comentario