ANÁLISIS DE VARIANZA DEL DISEÑO AL COMPLETO AZAR EN
GEOGEBRA
Ing. Luis Manfredo Reyes
El diseño al completo azar, también conocido como Al Irrestricto azar, de una vía o Oneway, es el más sencillo de todos los diseños experimentales disponibles, pero tiene el inconveniente que para su utilización se requieren condiciones homogéneas en el sitio experimental (por ejemplo: laboratorio).
El diseño se puede manejar con iguales repeticiones (balanceado) o desiguales (desbalanceado).
Es posible realizar el análisis en GEOGEBRA
GeoGebra es
un software matemático. Fue creado con la idea de ser usado para la educación en colegios y universidades.
Fue creado por Markus Hohenwarter, en el año 2001 en la Universidad
de Salzburgo, luego en la Universidad de Atlantic, Florida, luego en la Universidad Estatal de Florida y actualmente , en la Universidad de Linz, Austria.
El software tiene dos
partes importantes: un procesador geométrico y un procesador algebraico.
GeoGebra permite el
trazado de construcciones geométricas de todo tipo así como la representación
gráfica, el tratamiento algebraico y el cálculo de funciones reales de variable
real, sus derivadas, integrales, etc.
DISPONIBILIDAD:
Existen versiones para:
Windows, Linux, MacIntosh, Android e Ios.
Existen algunas diferencias
entre las versiones, pero la mayoría de aspectos son iguales.
La última versión disponible
es la 5.
En éste artículo se muestran
aplicaciones del Geogebra en el tema del diseño al completo azar, partiendo de
un ejemplo clásico de cualquier curso
del tema.
Se asume que el usuario tiene
instalado el programa y conoce el uso básico del mismo
Se asume que el
lector tiene instalado el paquete y conoce el uso básico del mismo.
A continuación un ejemplo :
Se
quiere evaluar la eficacia de distintas dosis de un fármaco contra la
hipertensión arterial, comparándola con la de una dieta sin sal.
Para ello se seleccionan al azar 25 hipertensos y
se distribuyen aleatoriamente en 5 grupos. Al primero de ellos no se le
suministra ningún tratamiento, al segundo una dieta con un contenido pobre en
sal, al tercero una dieta sin sal, al cuarto el fármaco a una dosis
determinada y al quinto el mismo fármaco a otra dosis.
resultados finales:
resultados finales:
En geogebra hay dos
formas de realizar el análisis: Desde a hoja de cálculo y desde la vista
algebráica
DESDE LA
HOJA DE CÁLCULO
Los datos se ingresan una columna por tratamiento:
Se da click sobre la
letra A al inicio de la primera columna
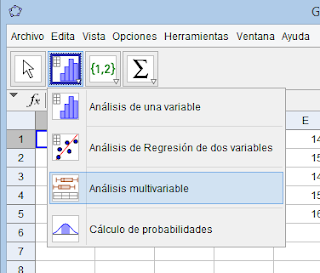
Luego se da click sobre
el ícono de las barras y se selecciona análisis mutivariable
Se da click sobre el
ícono de una manita, luego sobre el signo + cuatro veces.
Se señala la Letra B de
la segunda columna y luego se da click sobre el ícono de la manita en la
segunda columna y se hace lo mismo con las demás
Se da click sobre el
botón Analiza, aparece un gráfico de cajitas que muestra cada tratamiento y su
comportamiento.
Se da click sobre el
símbolo de sumatoria y aparecen los promedios y varianzas de cada tratamiento.
Se da click sobre el botón Estadísticas y se selecciona Anova
1.
Y aparece el resumen del
análisis de varianza
Como en casi todos los
programas estadísticos, no aparece la F de la tabla, sino el valor de p.
Si el valor de p es menor
a 0.05, se rechaza la hipótesis al 5% de significancia
Si el valor de p es menor
a 0.01, se rechaza la hipótesis al 1% de significancia
Si el valor de p es mayor
al nivel de signficancia deseado, se acepta la hipótesis
En este casi se rechaza
la hipótesis nula (que todos los tratamientos son iguales)
DESDE LA VISTA ALGEBRAICA
Se deben crear una lista
para cada tratamiento
L1={180,173,175,182,181}
L2={172,158,167,160,175}
L3={163,170,158,162,170}
L4={158,146,160,171,155}
L5={147,152,143,155,160}
Y luego se ingresa ésta
orden:
Anova[L1,L2,L3,L4,L5]
El programa no realiza
pruebas de medias (Tukey o Duncan).








No hay comentarios:
Publicar un comentario