VISUALIZACIÓN Y CÁLCULO DE
VOLÚMENES DE SÓLIDOS DE REVOLUCIÓN CON GEOGEBRA
Reyes
Chàvez, Luis
Ares
Físico-Matemática
Facultad
de Ciencias Químicas y Farmacia USAC
luismanfredo2000@gmail.com
Uno de los temas
màs difíciles en la enseñanza del càlculo integral es el del càlculo de
volúmenes de sòlidos de revoluciòn, debido a la dificultad de visualizar los
sòlidos, que requiere en muchos casos bastante imaginación.
Entre las opciones disponibles para
aplicar la informática en la enseñanza, se tiene Geogebra
GeoGebra es
un software matemático. Fue creado con la idea de ser usado para la educación en colegios y universidades.
Fue creado por Markus Hohenwarter, en el año 2001 en la Universidad
de Salzburgo, luego en la Universidad de Atlantic, Florida, luego en la Universidad Estatal de Florida y actualmente , en la Universidad de Linz, Austria.
El software tiene dos
partes importantes: un procesador geométrico y un procesador algebraico.
GeoGebra permite el
trazado de construcciones geométricas de todo tipo así como la representación
gráfica, el tratamiento algebraico y el cálculo de funciones reales de variable
real, sus derivadas, integrales, etc.
DISPONIBILIDAD:
Existen versiones para:
Windows, Linux, MacIntosh, Android e Ios.
Existen algunas diferencias
entre las versiones, pero la mayoría de aspectos son iguales.
La última versión disponible
es la 5.
En éste artículo se muestran
aplicaciones del Geogebra en el tema de visualización y cálculo de volúmenes de
sólidos de revolución., partiendo de
ejemplos clásicos de cualquier curso que aborde éste tema.
Se asume que el usuario tiene
instalado el programa y conoce el uso básico del mismo
Existe un archivo de hojas de trabajo de Geogebra
desarrollado por usuarios colaboradores de todo el mundo, llamado GEOGEBRA TUBE . Entre ellos, hay
varios dedicados al tema. Para ingresar a Geogebra tube se requiere conexión a
internet. Se puede ingresar desde internet, vía navegador, o bien desde la misma aplicación.
MÉTODO DE LOS DISCOS
ROTANDO EN EL EJE X
Al iniciar sesión de trabajo en Geogebra,
Se ingresa a Archivo y luego Abrir desde Geogebra tube:
en la casilla de búsqueda se ingresa: Sólido de revolución,
de todas las opciones que aparecen, se selecciona el elaborado por el usuario Instituto Geogebra de Celaya.
La hoja puede ser almacenada en la computadora local.
En éste caso, la función gira alrededor del eje x.
Se aplica el método de los discos para aproximar el volumen.
La variable n es un deslizador, que puede ser movido a voluntad para definir el
número de discos.
Se ingresa la función a trabajar y se definen los límites de
integración en la gráfica que aparece en la vista de dos dimensiones
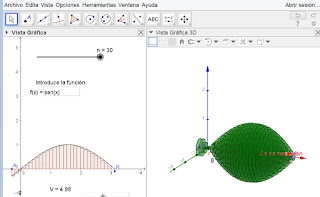
Por ejemplo: (Gráfica del pecesito)
Visualice y calcule el volumen del sólido resultante cuando
la gráfica de y= sen x rota alrededor del eje x, entre x=-1 y x=π. Pruebe con
diferentes valores de n y compare resultados.
Con n=10
Con n=20
Con n=30
El valor exacto del volumen calculado con una integral es:
Integral[pi*sen(x)^2,x,-1,pi], en la vista algebraica, que
da como resultado: 5.791437
ROTACIÓN EN EL EJE X CON DOS FUNCIONES
Se ingresa a Geogebra Tube y se localiza la hoja de trabajo
llamada: Calculadora de sólidos de revolución de Daniel Vásquez.
Se debe ingresar la función que pasa arriba (f), si hay otra
función se marca la casilla que dice sólido con hueco? Y se ingresa la función.
Luego se ingresan los límites de integración.
Ejemplo:
La regiòn formada
por y=x2+1, y=x+3 rota sobre el eje x. Calcule el Volumen del sòlido
resultante
Primero hay que encontrar los límites de integración, para
lo cual en la vista algebraica se ingresa:
Interseca[x^2+1,x+3]….. el resultado es: (-1,2) , (2,5)
La hoja de trabajo es la siguiente
ROTACIÓN SOBRE EL EJE Y
Se debe localizar en Geogebra Tube la hoja de trabajo: Solids
of revolution del autor Ken Schwartz
Ejemplo:
La región formada por: y= x2-3 y y=x rota sobre
el eje y. Calcule el volumen del sólido resultante
Se ingresan los datos, y se da click sobre el botón spin it!
Se puede ajustar la transparencia (Trans), que muestre o no
las arandelas, y la posición
Los puntos rojos sobre el eje x se deben ajustar para que
concidan con los interceptos de la gráfica





No hay comentarios:
Publicar un comentario